Homework Assignment #4

Due Monday, November 25, 11:59 PM
43 points total

1. (15 points) Shortest Path on a Map  - Write in Python

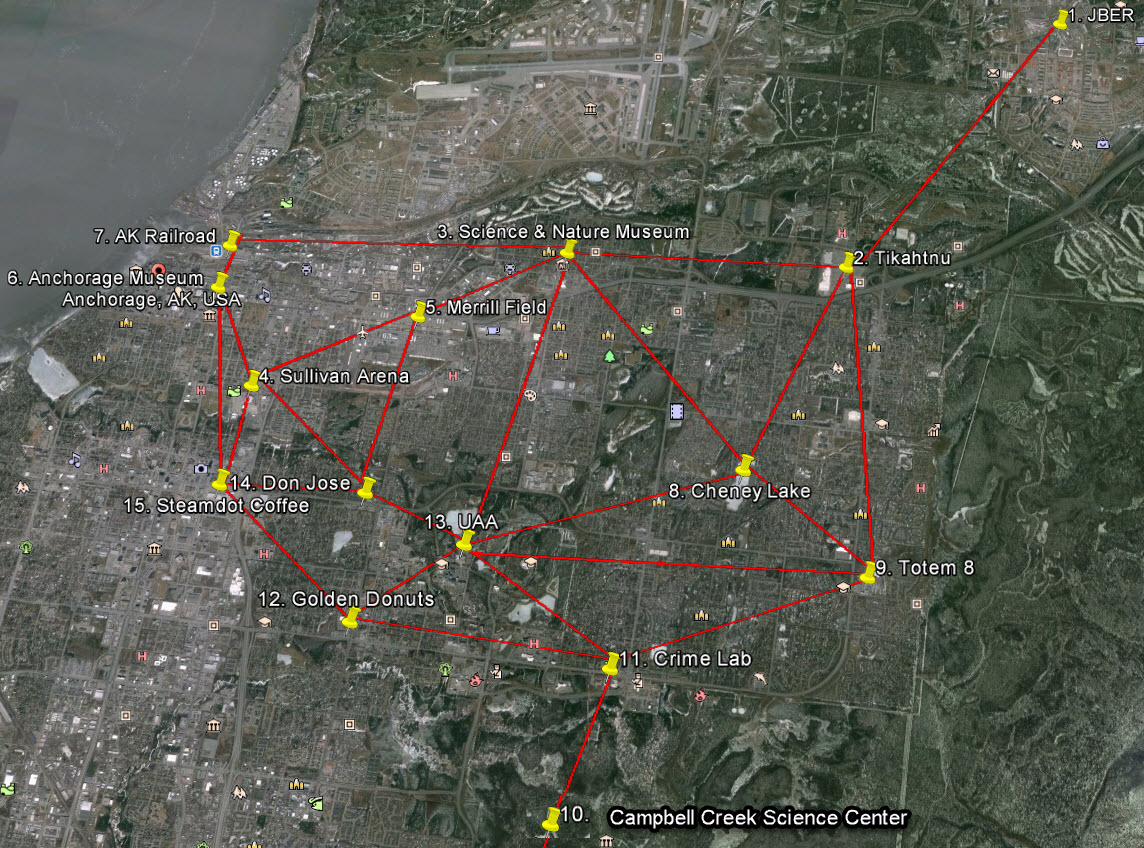
The map below represents a crude graph of places around Anchorage. Each location is a node. The red lines indicate edges between nodes. The edges have weights, which is the distance between the nodes. All of this information is stored in the data below, which you can save in a text file and read into your program.

The format of the file is:

Line 1: Number of nodes in the file

The following then repeats for the number of nodes in the file:

Number of node (e.g. 1 on the map)
Name of node (e.g. "JBER" on the map)
Number of edges from this node
NeighboringNodeNumber  WeightOfEdgeToNode
... (repeats for the number of edges)

In the data below, Tikahtnu is node number 2 and has 4 edges. It is connected to Node 1 with weight 2.71, Node 3 with weight 2.21, Node 8 with weight 1.8, and Node 9 with weight 2.39

15
1
JBER
1
2 2.71
2
Tikahtnu
4
1 2.71
3 2.21
8 1.80
9 2.39
3
Science & Nature Museum
5
2 2.21
5 1.19
7 2.60
8 2.18
13 2.40
4
Sullivan Arena
4
5 1.31
6 0.79
14 1.25
15 0.76
5
Merrill Field
3
3 1.19
4 1.31
14 1.45
6
Anchorage Museum
3
4 0.79
7 0.41
15 1.58
7
AK Railroad
2
3 2.60
6 0.41
8
Cheney Lake
4
2 1.80
3 2.18
9 1.25
13 2.09
9
Totem 8
4
2 2.39
8 1.25
11 1.89
13 2.90
10
Campbell Creek Science Center
1
11 1.61
11
Crime Lab
4
9 1.89
10 1.61
12 1.89
13 1.38
12
Golden Donuts
3
11 1.89
13 0.94
15 1.40
13
UAA
6
3 2.40
8 2.09
9 2.90
11 1.38
12 0.94
14 0.81
14
Don Jose
4
4 1.25
5 1.45
13 0.81
15 1.02
15
Steamdot Coffee
4
4 0.76
6 1.58
12 1.40
14 1.02
        

2. (12 points) Minimum Spanning Tree on a Map - Write in Python

Using the same graph as problem 1, write a program that calculates a Minimum Spanning Tree and output the edges and total edge weight of the MST. The MST could be used if you wanted to connect all the nodes in some way (e.g. water, electrical network connection). Your program can use any MST algorithm that you like as well as the data structures of your choice for internal implementation (e.g. making a set or queue).

3. (8 pts) Insertion sort on small arrays in merge sort:

Although merge sort runs in O(nlgn) time, and insertion sort runs in O(n^2) time, the constant factors in insertion sort make it faster for small n. Thus, it makes sense to use insertion sort within merge sort when subproblems become sufficiently small. Consider a modification to merge sort in which n/k sublists of length k are sorted using insertion sort and then merged using the standard merging mechanism, where k is a value to be determined.

1. Show analytically (not empirically through a program) that the n/k sublists, each of length k, can be sorted by insertion sort in O(nk) worst-case time.
2. Show that the sublists can be merged in O(n lg(n/k)) worst-case time.
3. Given that the modified algorithm runs in O(nk + nlg(n/k)) worst case time, what is the largest asymptotic (O notation) value of k as a function of n for which the modified algorithm has the same asymptotic running time as standard merge sort?
4. How should k be chosen in practice?

4. (8 pts). Mystery Sort.

Analyze the following sorting algorithm and determine its runtime. Hint: Output the array in the isSorted method. What would be an appropriate name for this sorting algorithm?

# True if array a is sorted
def isSorted(a):
    for i in range(len(a) - 1, 0, -1):
        if (a[i] < a[i-1]):
            return False
    return True

# Swaps two elemeents in the array
def swap(a, i, j):
    t = a[i]
    a[i] = a[j]
    a[j] = t

# Where the magic happens to sort an array a. n is the end index
# of the data we are sorting.
def sort(a, n):
    if (n == 1):
        return isSorted(a)
    for i in range(0, n):
        swap(a, i, n-1)
        if (sort(a, n-1)):
            return True
        swap(a, i, n-1)
    return False

# Sample sort
a = [5, 3, 2, 6, 4]
sort(a, len(a))
print(a)